Return Wave Calculations


Take a look at the first positive pulse in the exhaust port pressure trace shown below. It almost looks exactly like a sine wave. It isn't a square wave due to the fact that most exhaust ports are roundish and as the piston uncovers the port the area of flow gradually increases, not all at once. Blair wrote that a pressure wave travelling in a pipe will have its peak travel a little faster than the rest of the pulse so that, given enough length, this exhaust pulse will be just like a sine wave. So I use a sine wave in my calculations to represent the exhaust pulse. At 30 degrees a sine wave has 50% strength, at 60 degrees 87%, and at 90 degrees 100%. So for the illustration example below I use these numbers to represent the varying pressures of a sine wave shaped pressure pulse: 0, .5, .9, 1, .9, .5, 0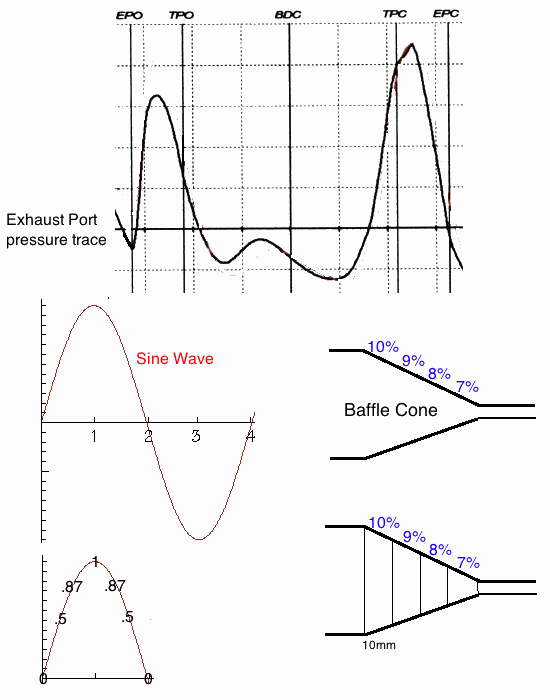
 

Blair also said that the change of area along an expansion chambers cones is the cause of the return waves with more change causing more return wave strength. For illustration purposes I have depicted a baffle cone with area changes ranging from 10% to 7%.
Now look at the illustration below. The red numbers are those of the exhaust pulse, and the blue numbers are the percentages of baffle cone area change. As the exhaust pulse traverses the baffle cone we will multiply the red and blue numbers to derive the black numbers below. Looking at the third step, where the exhaust pulse has reached the 30mm length of the baffle cone, we can see the return wave has the strengths of 0 and 5. At the 7th step, at top right of illustration, the return wave progresses in strength from 0 to 18. The final step is at the bottom right. Hopefully this example makes it obvious that wave strength steps are combining to make the final version of the return wave. Look at the 7th step and see how the 4th "strength" of return wave is a combination of 10 and 4.5 to result in 14.5. The next strength is 9 + 8.1 to equal 17.1. So when you want to calculate for 12 sections of exhaust pulse traveling through a 190mm long baffle cone it is just a mind-bender to try to do so without a calculator such as Excel.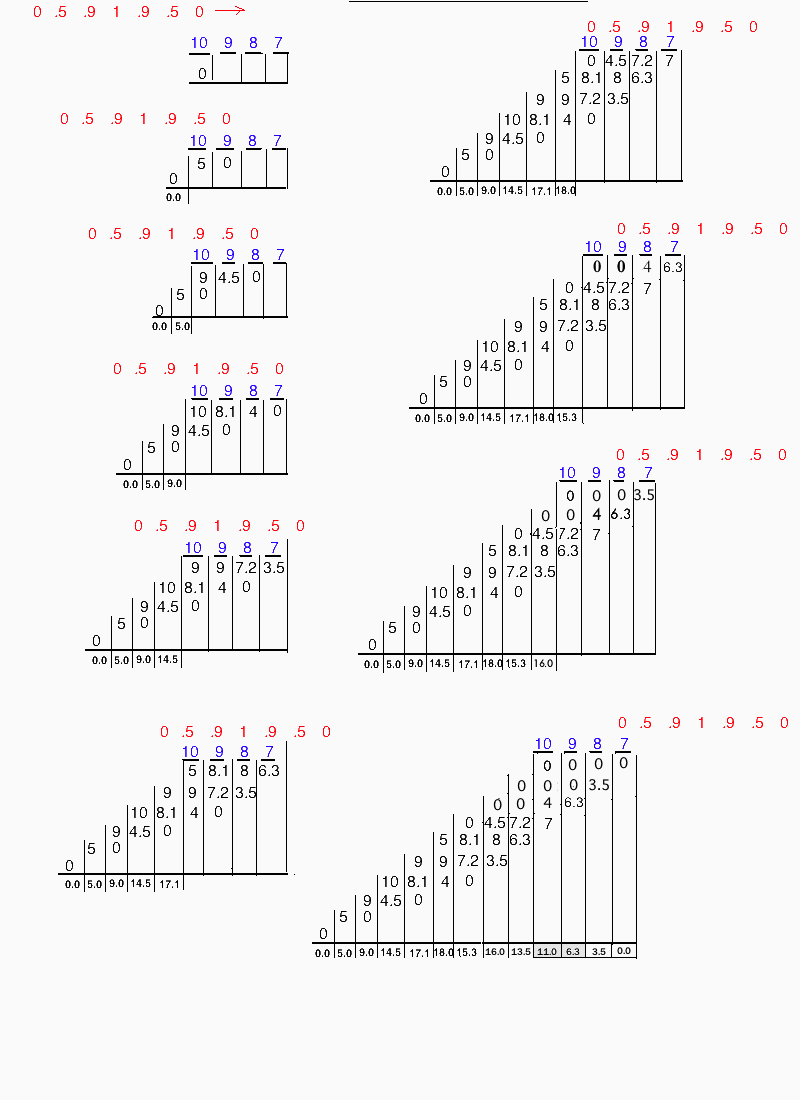
 


The final step shows the return wave having these strength numbers: 0, 5, 9, 14.5, 17.1 18, 15.3, 16, 13.5, 11, 6.3, 3.5, 0. The graph of these numbers showing the shape and width of the return wave is shown below: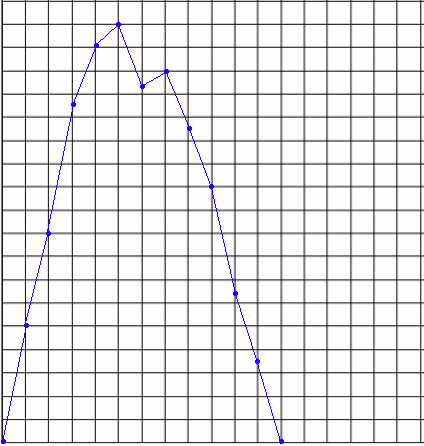
 


Here is the formula (shortened to not bore you) for one of the many stages of baffle return wave calculation from my Excel file that is a byproduct of this knowledge of how multiple mini-reflections combine to make the final return wave:
=(B7*C13+B8*C11+B9*C9+B10*C7)*-0.00235
The last number is a correction factor.
What is strange is that  each wave has a trailing wave of smaller strength and opposite polarity. So the exhaust pulse has a "tail" of a negative pressure pulse with 39% of its width and 25% of its height. This tail also has to be added into the calculations because it shortens the return wave a bit. Also the diffuser return wave has a tail that affects the beginning of the baffle wave when the two waves are graphed together. These are some of the reasons that it is impossible to really know the return waves without this type of calculator. People that rely on just formulas are only getting close. Perfection can only had by this type of system.

UPDATE
ECcalc version 24 and on up varied from the previous description in that instead of purely using the area change, it uses the area change as part of a formula (Boyles Law) that determines the pressure difference per area change. Before the assumption was that the return wave strength was in direct relation to the area change but now I know that the return wave is dependant on the pressure change as the pressure wave travels along the diffuser or baffle. This corrects the inaccuraacy that happens when the belly is more than 6.25 times the area of the header. All in all it is a more accurate method. Below you can see that the pressure to area change is anything but linear.




 

HOME